2184E 寻找有多少个子数组满足 k-exquisite,即相邻数字的差 > k。对任意 k [0, n-1] 都要有个解。
题解
不难想到 k 可以从大到小构建。
先新建差分数组,再按照其值从大到小排序,差分值为第一关键字降序, pos 第二关键字升序 我们发现,比如假设我们算好了 k = n - 1,当 k = n - 2 的时候,可以通过算贡献的方式,计算出新增的贡献。
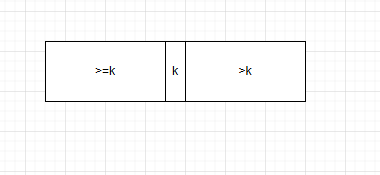
可以发现当我们做到 k 时,我们从左到右枚举前面的 >= k 连续段任意一个 lpos 都会作为左端点,k 作为右端点,成为一个贡献。 而右边大于 k 的连续的都可以作为右断点, k 和 k 左边的 >= k 的连续段作为右断点。假设 k 左边的满足 >=k 的连续段长度为 l,右边连续段满足 >k 的的长度为 r。那么新增的贡献为 (lok + 1 + rok * (lok + 1))。
考虑边界情况,即 k = n - 1 的时候,我们发现这种规律也试用。
(但是思考时,我是先考虑左右都大于 k,然后考虑边界情况,扩展得到左边 >= k,右边 > k 的)
代码:
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 1e5 + 100;
int f[maxn],h[maxn], sz[maxn];//每个结点的父亲及树高
//初始化n个元素
void init(int n)
{
for(int i = 1; i <= n; ++i)
{
f[i] = i;
h[i] = 0;
sz[i] = 1;
}
}
//查询树的根
int find(int x)
{
if(f[x] == x) return x;
else return f[x] = find(f[x]);//路径压缩
}
//合并x和y所属的集合
void unite(int x, int y)
{
x = find(x);
y = find(y);
int szx = sz[x];
int szy = sz[y];
if(x == y) return;
//树高优化,由于find后已经路径压缩,所以x与y的高度差最多为1
if(h[x] < h[y]) f[x] = y;//这里树高相差1(一个为1,一个为0),合并后x与y的高度都不变
else
{
f[y] = x;
if(h[x] == h[y]) h[x]++;//这里树高相等,合并后父亲高度加1
}
sz[find(x)] = szx + szy;
}
int get_l(int pos, int diff, vector<int>& raw_diff, int n) {
if (pos == 1) {
return 0;
} else if (raw_diff[pos-1] < diff) {
return 0;
} else {
return sz[find(pos-1)];
}
}
int get_r(int pos, int diff, vector<int>& raw_diff, int n) {
if (pos == n) {
return 0;
} else if (raw_diff[pos+1] <= diff) {
return 0;
} else {
return sz[find(pos+1)];
}
}
void solve() {
int n;
cin >> n;
init(n + 20);
vector<int> v(n+1);
for (int i = 1; i <= n; i++) {
cin >> v[i];
}
vector<pair<int,int>> rank;
vector<int> diff(n+1);
for (int i = 1; i <= n - 1; i++) {
diff[i] = abs(v[i] - v[i+1]);
rank.push_back({abs(v[i] - v[i+1]), -i});
}
sort(rank.begin(), rank.end());
reverse(rank.begin(), rank.end());
rank.push_back({-1, -1});
vector<int> ans(n+1, 0);
int tot_at_this_stage = 0;
int tot = 0;
int last_diff = n;
for (const auto [vdiff, pos_rev]: rank) {
const int pos = -pos_rev;
if (vdiff != last_diff) {
tot += tot_at_this_stage;
tot_at_this_stage = 0;
for (int i = last_diff; i > vdiff; i--) {
ans[i] = tot;
}
last_diff = vdiff;
}
const int lok = get_l(pos, vdiff, diff, n);
const int rok = get_r(pos, vdiff, diff, n);
tot_at_this_stage += (lok + 1 + rok * (lok + 1));
if (lok > 0) {
unite(pos, pos - 1);
}
if (rok > 0) {
unite(pos, pos + 1);
}
}
tot += tot_at_this_stage;
for (int i = last_diff; i >= 1; i--) {
ans[i] = tot;
}
for (int i = 1; i <= n- 1; i++) {
cout << ans[i] << " ";
}
cout << endl;
}
signed main() {
int T;
cin >> T;
while (T--) solve();
}